Apa itu Matriks?
Pengertian matriks adalah kumpulan bilangan (atau unsur) yang disusun menurut baris dan kolom tertentu. Bilangan-bilangan yang disusun tersebut dinamakan eleme-elemen atau komponen-komponen matriks. Nama sebuah matriks biasanya dinyatakan dengan huruf kapital. Dalam sebuah matriks ada istilah ordo. Yang dimaksud dengan ordo atau ukuran matriks adalah banyaknya baris x banyak kolom dalam sebuah matriks.
Contoh :

Sama halnya dengan penjumlahan, pengurangan dapat dilakukan hanya jika dua matriks atau lebih, memiliki ordo yang sama. Pengurangan dilakukan terhadap elemen-elemen yang berposisi sama.
Contoh:
Jika 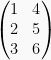 dan
dan 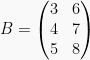 ,
,
maka:
Sifat dari penjumlahan dan pengurangan matriks:
- A + B = B + A
- (A + B) + C = A + (B + C)
- A – B ≠ B – A
Perkalian Matriks
Matriks dapat dikalikan dengan sebuah bilangan bulat atau dengan matriks lain. Kedua perkalian tersebut memiliki syarat-syarat masing-masing.
Perkalian Matriks dengan bilangan bulat
Suatu matriks dapat dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka 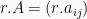 . Contoh:
. Contoh:
Jika 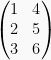 dan bilangan r = 2, maka:
dan bilangan r = 2, maka:
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks dapat dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:
- r(A + B) = rA + rB
- r(A – B) = rA – rB
Perkalian dua matriks
Perkalian antara dua matriks yaitu matriks A dan B, dapat dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian tersebut menghasilkan suatu matriks dengan jumlah baris sama dengan matriks A dan jumlah saman dengan matriks B, sehingga:

Download Modul









